DATAMATH CALCULATOR MUSEUM
|
DATAMATH CALCULATOR MUSEUM |
Texas Instruments TI-30XA (2009)
| Date of introduction: | January 2009 | Display technology: | LCD |
| New price: | $10.99 (SRP 2009) | Display size: | 10 + 2 |
| Size: | 5.9" x 3.0" x 0.50" 150 x 75 x 13 mm3 |
||
| Weight: | 2.9 ounces, 82 grams | Serial No: | |
| Batteries: | 2*LR44 | Date of manufacture: | mth 01 year 2009 (F) |
| AC-Adapter: | Origin of manufacture: | China (K) | |
| Precision: | 12 | Integrated circuits: | |
| Memories: | 3 | ||
| Program steps: | Courtesy of: | Joerg Woerner |
Texas
Instruments released rather silent in January 2009 the TI-30XA with larger
digits and even in September 2009 most stores in Upstate New York carry a mix of
"old" and "new" calculators in their shelves. The only
visible difference for the customer is a small sticker "New
Larger Digits!" on the sales box.
In Europe a solar powered version of the TI-30XA is sold as
TI-30 ECO RS, it was upgraded to the larger
digits, too.
A
first inspection of the revised TI-30XA confirms indeed a nice display with
bold, huge digits and even without placing two calculators side-by-side we
recognized the improvement immediately.
Disassembling
this TI-30XA manufactured in January 2009 by Kinpo Electronics,
Inc. in China reveals no surprises. The printed circuit board (PCB) of the
calculators sports still a prominent SR-30 logo - with a revision index of 12. A
TI-30XA calculator manufactured five years
earlier by Kinpo Electronics, Inc. carried e.g. the SR-30-10 designator.
In 2013 Texas Instruments introduced again a
TI-30Xa - using identical electronics in a newly
designed housing.
Since its introduction in 1996 we verify with each TI-30Xa
the presence of the Logarithm Bug
and - yes....
The
algorithm problem known as "Logarithm Bug" was implemented already
1991 with the TI-35X and TI-36X
SOLAR and floats around in various calculators.
The best way to demonstrate the logarithm bug could
be found with the exponential function, one of the most important
functions in mathematics. It is written as ex and can be
defined as a limit of a sequence:
 |
The calculation of this expression
will yield to unexpected results due to:
• The ln(1 + x) problem |
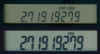
Using
n=109 should reveal a very close approximation of ex=2.71828183
(rounded to 9 digits) but this TI-30XA manufactured in 2009 still indicates 2.71919279.
If you have additions to the above article please email: joerg@datamath.org.
© Joerg Woerner, November 16, 2009. No reprints without written permission.